加重平均と重み
加重平均は、英語名「Weighted Average」からも分かる通り、「重み ( ウエイト )」を加味した平均値になります。
教科書的な数式を示すと、次の通りです。

ちなみに、重みを加味しない ( 全ての重みが等しい ) 場合は、普通の平均値 ( 算術平均 ) になります。
上記の式の重み ( W ) に、1を代入すると普通の平均であると分かるでしょう。
この「重み」という言葉が出てくるせいで、我々の理解を邪魔してきます。
しかし、内容を確認すると難しい計算はなく、無意識に使ったことがある人も多くいるような計算です。
まず、「重み」をよりイメージしやすい言葉に変えると、
「全体のデータ数の内、各 X ( 観測される値 ) に該当するデータ数」です。
全体のデータ数が100で、X1に該当するデータ数が20なら、W1 (X1の重み) は20です。
なお、イメージのため「データ数」と言いましたが、整数である必要はありません。
あくまで、全体( 分母 )の内、どの程度が各 X に該当するかを表現できれば問題ないです。
具体的な計算については、後の「加重平均の具体例」の項目で説明します。
ここでは、もう少し、加重平均の式に着目してみましょう。
先程、加重平均の数式は次のように示しました。

この式を、次のように変形してみます。
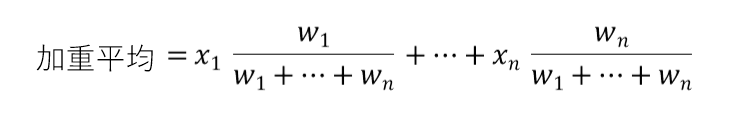
ここで、各 X に掛けている分数は、X が占める割合を示しています。
つまり、加重平均は、
各観測される値 ( X ) に、その「シェア」をかけた合計値とも表現できます。
加重平均の具体例
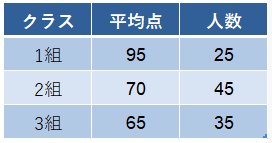
成績の良し悪しでクラス決めをする予備校で、テストを行いました。
その結果とクラスの人数は、下記の通りです。
1組~3組全体の平均点は、いくらでしょうか。
この計算をするときに、皆さん無意識に、加重平均を使います。
普通の平均値は、( 95+70+65 ) / 3 ≒76.67点ですが、誤りであることは理解できるでしょう。
各クラスの、人数の違いを考慮していないからです。
この「人数の違い」が、「重みの違い」というわけです。
加重平均の式に当てはめると、74.75点が求まります。

この点数が、1組~3組全体の平均点です。
また、加重平均は式変形すると、
各観測される値 ( X ) に、その「シェア」をかけた合計値とも表現できます。
その場合の計算結果も、もちろん同じ値となります。
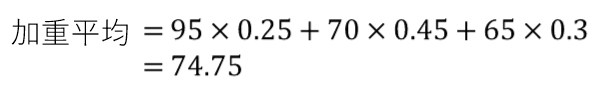
ここでいう「シェア」とは、
「全クラスの内、各クラスが占める人数の割合」のことです。
加重平均の特徴
これまでに示した、計算式からも分かるように、
加重平均は、重みが大きいデータに引っ張られる特徴があります。
前項のテストの例ですと、平均95点と優秀な1組の成績からは遠い、
「加重平均=74.75点」という結果になりました。
70点付近を取った、2組、3組の影響を大きく受けていますが、
その原因は、2組、3組の人数が、全体の75%を占めているからです。
このように、重みが大きいデータに引っ張られる特徴は、
加重平均の値を確認するときに、留意する必要があります。
TOPIX ( Tokyo Stock Price Index ) とは
ここからは、実社会で使用されている加重平均の話になります。
加重平均が使われている「TOPIX」とは、
「東証株価指数」という指数で、一部上場全銘柄を対象に算出されています。
「日経平均株価」と並ぶ有名な株価指数で、
株式市場の様子を把握するために、重要な指標となっています。
また、TOPIXに連動した投資商品も存在します。
TOPIXの計算方法
1968年1月4日を基準日に、当時の時価総額を100として、
現在の時価総額がいくらになるかという点に着目して計算されます。
その際、TOPIXの変化率は、一部上場全銘柄について、
「全会社の時価総額に占める、各会社の時価総額」を重みとして加重平均で計算されます。
TOPIX投資時の留意点
加重平均の特徴については、重みが大きいデータに引っ張られることを説明しました。
加重平均を利用するTOPIXについても、この特徴があります。
つまり、重みの大きな、
時価総額が大きい会社の株価に影響されやすいということです。
今後、TOPIX連動の投資商品が伸びるかは、
時価総額の大きい会社 ( 業界 ) がさらに伸びるのかに影響しやすいと言えますね。
業種別時価総額を確認したい場合は、下記外部リンクからどうぞ。
まとめ
これまで、加重平均について説明してきました。
加重平均は、「重み ( ウエイト )」を加味した平均値になり、
その性質故、重みが大きいデータに引っ張られる特徴があります。
複数の平均値から、全体の平均値を算出する際など、
無意識のうちに使っているような計算でしたね。
また、実社会においては、TOPIXという株価指数の算出に使われています。
ニュース番組でTOPIXが出た際は、この記事を思い出してくれたら、嬉しい限りです。
それでは、最後まで読んでいただきありがとうございました!








コメント