正規分布とは
正規分布の概要
正規分布は、量的変数の分析で、最もよく観察される分布です。
( 量的変数・・・例えば、身長のような数値データ )
英語での記載は「normal distribution」、つまりは「普通の分布」です。
この分布は、仮説検定などで利用されたり、他の分布の基礎ともなります。
様々な場面で目にするので、統計学を学ぶ上で、避けては通れない分布と言えます。
正規分布の確率密度関数と分布の外観
分布の確率密度関数は、次の通りです。

また、分布の外観は、次のようになります。( 詳細は、後述とします )
正規分布の具体例
正規分布に従うと考えられるものには、次などがあります。
・同年代の身長
・あなたの平日の睡眠時間
・ある製品のサイズ
・ある製品の耐久年数
おおよその平均値のイメージがついて、そこに誤差 ( 個体差 ) があるものは、正規分布に従っていると考えて大きな間違いはないでしょう。
また、次のものは「中心極限定理」に従い、正規分布となることが分かっています。
・サンプルの平均値
【補足】中心極限定理
この定理は、「母集団の分布の形状によらず、そこから抽出した標本の平均値は、正規分布に従う」というものです。
なお、平均値算出の際のデータ数(標本サイズ)は、大きいほど正規分布に従います。
具体例についても確認したい方は、下記の記事を参考にしてください。
2つの決定因子 ~平均値と分散~
確率密度関数からも分かる通り、正規分布の形状を決定する因子は、μ ( 平均値 ) とσ^2 ( 分散 ) の2つです。
従って、正規分布については、「N ( μ , σ^2 )」と表記します。
( 「N」は、正規分布の英語「normal distribution」から )
それぞれの値が、分布の形状に与える影響について、見ていきましょう。
平均値が変わるとどうなるか
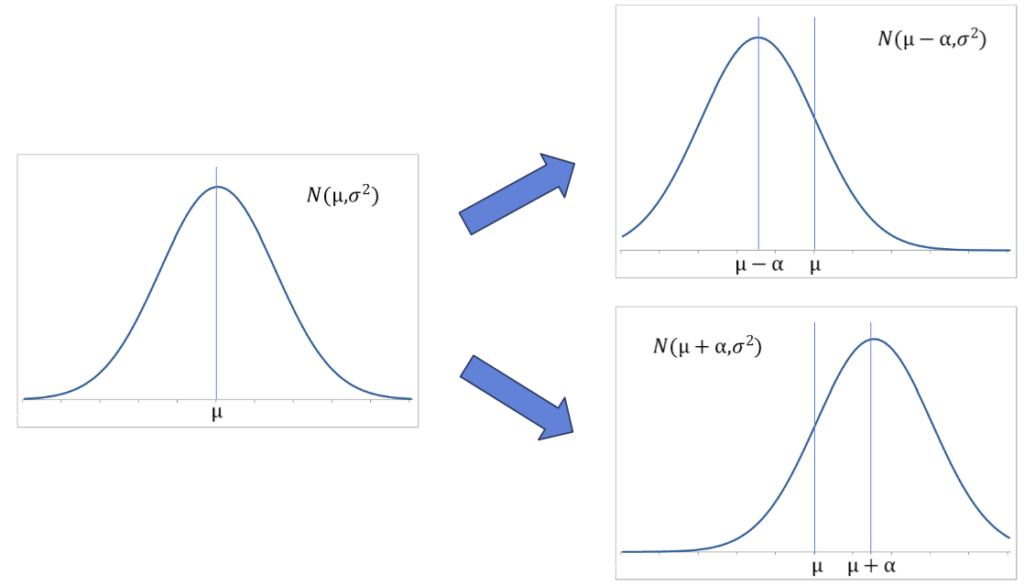
平均値が変わる場合、分布の形はそのままに、位置が左右にスライドします。
正規分布において、平均値は最頻値と一致しますので、グラフの頂点部分は平均値と重なります。
ここから、「平均値が動くと分布の位置も連動する」とイメージすると覚えやすいですね。
分散が変わるとどうなるか
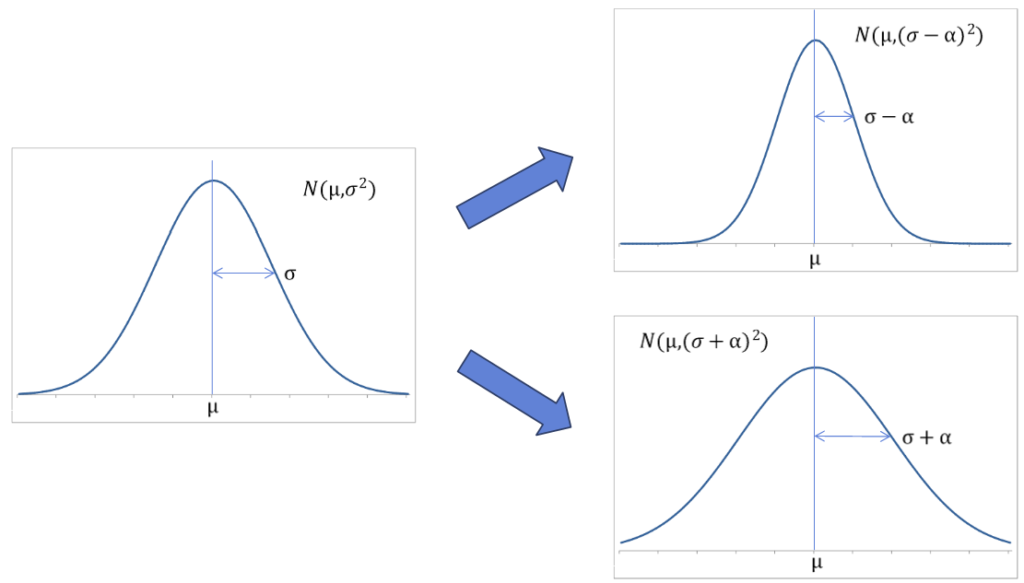
分散が変わる場合、位置はそのままに、分布の形( とがり具合 )が変わります。
そもそも分散というのは、平均値からの散らばり具合を表す統計量です。
この値が小さくなると、より平均値周辺にデータが集まり、
値が大きくなると、より平均値から離れたところでデータがみられるようになります。
分散の定義そのままなので、挙動のイメージも覚えやすいでしょう。
標準偏差との関係
データが正規分布に従う場合、理論上、次のことが言える。
・平均値±σの範囲( ピンク色 )に、データ全体の約68%含まれる。
・平均値±2σの範囲( ピンク色+赤色 )に、データ全体の約95%含まれる。
・平均値±3σの範囲に、データ全体の約99%含まれる。
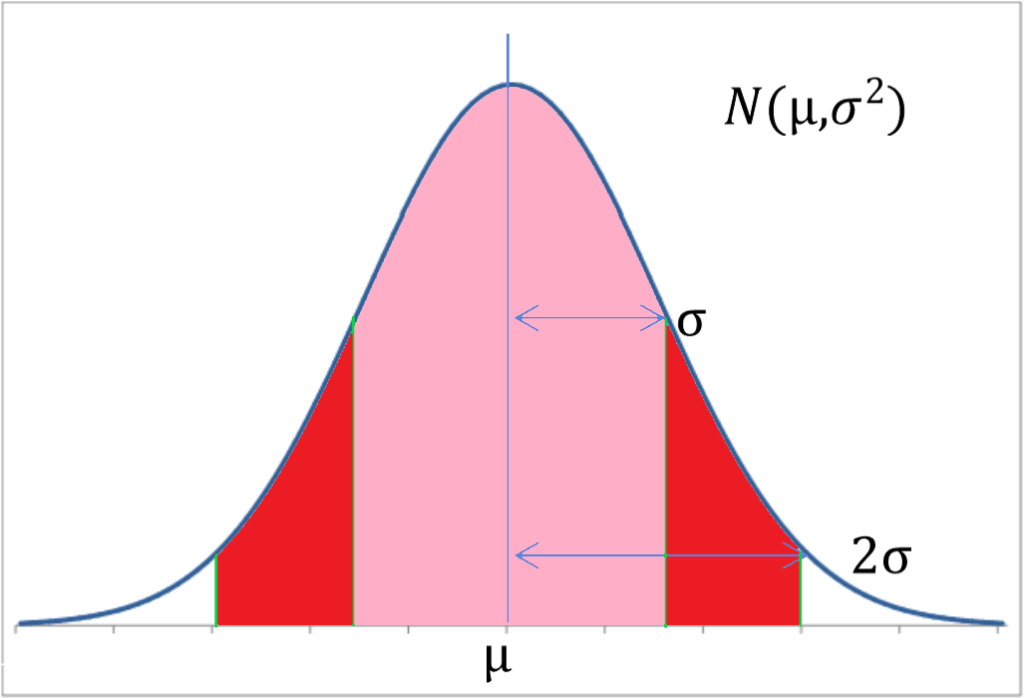
一般的に、平均値±2σの範囲を超えるデータについては、かなり珍しいデータとされています。
これは、データ全体の5%しか該当しないため、感覚的にも珍しいことは分かると思います。
例えば、とあるテストの結果が、次の場合を考えます。
平均値:60点 標準偏差:10点 ( ただし、正規分布に従うものとする )
このテストにおいて、85点を取った場合、
平均値±2σの範囲 (40点~80点)を超えているため、かなり優秀と言えます。
標準偏差について確認したい方は、下記の記事を参考にしてください。
また、テストに関しては、よく「偏差値」が算出されます。
「標準偏差」と「正規分布」の知識を持ったうえで、偏差値を見ると、
偏差値が意味していたことを、より理解することができます。
正規分布における標本平均
正規分布N ( μ , σ^2 )に従う標本について、
その標本平均は、N ( μ , (σ/√n)^2 )に従います。書き直すと、N ( μ , σ^2/n )です。
統計検定2級の練習問題にも出題されていたので、受検する場合は覚えておきましょう。
おわりに
今回、正規分布についていろいろと説明してきました。
様々な場面で目にするので、統計学を学ぶ上では必須の知識だと思いますので、
この記事で、正規分布についての理解が深まれば幸いです。
最後まで、読んでいただきありがとうございました!








コメント