標準偏差とは何か
標準偏差とは、値のバラツキ具合を表現する統計量になります。
データが、平均値から遠くまで散らばっていればいるほど大きな値を算出します。
標準偏差の求め方
標準偏差の計算式は、下記の通りです。

母集団の標準偏差( σ )も標本の標準偏差( s )も同様の式で算出できます。
計算方法を文章で説明しますと、次のようになります。
① データの平均値を算出する。
② 各データの値から、①で求めた平均値を引き、それを2乗する。
③ 全部のデータで②の処理を行ったら、すべて足し合わせる。
④ ③で得た値を、データの数で割る。※
⑤ ④で得た値のルートを算出する。
※①~④まで計算した値を「分散」と言います。
④の時に、(データの数-1)とする場合があります。
分散の式に従って、使い分ける必要がありますが、
ここでは、データ数で割る標準偏差について説明を続けます。
使い分けについては、以下を参考にしてください。
(余談ですが、データ数で割った標準偏差も、(データ数-1)で割った標準偏差も、
母標準偏差の不偏推定量ではありません。)
標準偏差の算出と考察
標準偏差の具体例
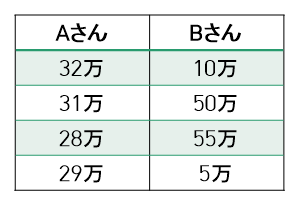
次のように、2人の月収があります。
ここから、前章の計算方法に則り、標準偏差を求めてみましょう。
① データの平均値を算出する。
Aさん:(32+31+28+29)÷4=30
Bさん:(10+50+55+5)÷4=30
② 各データの値から、①で求めた平均値を引き、それを2乗する。
Aさん:(32-30)^2=4、(31-30)^2=1、(28-30)^2=4、(29-30)^2=1
Bさん:(10-30)^2=400、(50-30)^2=400、(55-30)^2=625、(5-30)^2=625
③ 全部のデータで②の処理を行ったら、すべて足し合わせる。
Aさん:4+1+4+1=10
Bさん:400+400+625+625=2050
④ ③で得た値を、データの数で割る。
Aさん:10÷4=2.5
Bさん:2050÷4=512.5
⑤ ④で得た値のルートを算出する。
Aさん:√2.5≒1.58
Bさん:√512.5≒22.64
2人の標準偏差は、Aさんが「1.58万」、Bさんが「22.64万」となります。
標準偏差の特徴と考察
求めた標準偏差について、考察してみましょう。
一般的に、平均値から標準偏差±2個分を超えるデータについては、かなり珍しいデータとされています。
例えば、Aさんの次の月収が「32万」だったとします。
これは平均値から標準偏差±2個分の範囲(26.84~33.16万) の中に収まっているので、これまでの給料水準から考えても、珍しい値ではありません。
逆に、「35万」の月収だった場合は、これまでの給与水準から考えると珍しく高いと言えます。
Bさんについてはどうでしょうか。
Bさんの平均値から標準偏差±2個分の範囲は、-15.28~75.28万ですので、平均値の2倍にもなる「60万」を受け取れたとしても、珍しいことではありません。
また、多少赤字になることも珍しくはないと言えます。
Bさんタイプの収入の人は、Aさんタイプの収入の人より、備えをしっかりしないといけませんね。
【補足】
データが「正規分布」に従うことを仮定すると、平均値を軸に標準偏差±1個分の範囲に、約68%のデータが入り、標準偏差±2個分の範囲に、約95%のデータが入ります。
つまり、標準偏差±2個分を超えるデータについては、全体の約5%しかないことになります。
これは分布を仮定した場合のパーセンテージになりますが、平均値から標準偏差2個分より大きいデータ、小さいデータが、どの程度特殊かを理解することはできるでしょう。
標準偏差を使った身近な例
標準偏差を使った身近な例として、「偏差値」があります。
偏差値は、50を基準にして、次のように計算される指標です。
・平均値から標準偏差2個分高い成績なら、偏差値=70
・平均値から標準偏差1個分高い成績なら、偏差値=60
・平均値から標準偏差1個分低い成績なら、偏差値=40
・平均値から標準偏差2個分低い成績なら、偏差値=30
偏差値については、下記の記事で紹介しています。
おすすめ書籍
確率の知識や難しい記号をほとんど使わない、「超入門書」になります。
特に、標準偏差について力を入れて、解説している内容となっています。
私自身、初めて買った統計学の本ですが、
標準偏差や統計学の全体像について、しっかり把握することができました。
これから統計学を学ぼうとする方には、大変おすすめできる書籍です。
おわりに
月収については、安定していた方が便利です。
今月も同程度の収入が期待できるので、それを踏まえて、旅行やショッピングができますからね!
ただ、来月いきなり「50万」が必要になった時、2人とも貯金がなかったらどうでしょう。
Bさんは、今の仕事だけで獲得できる可能性がありますが、Aさんはまず無理です。このような状況であれば、標準偏差が大きく、爆発力のある方に軍配が上がりますね。
今回は、月収の平均値が同じ2人を例にしてみました。標準偏差が異なると、その意味合いが大きく変わってくることにお気付き頂けましたでしょうか。
今後は、「平均値」だけではなく、「標準偏差」についても注目してみてください!







コメント