幾何平均の求め方
幾何平均の求め方は、実にシンプルです。
掛け算して、掛け算した個数分のn乗根が幾何平均になります。
文章では、伝わりづらいので例示して説明します。
例①:「8」と「2」の幾何平均を求める
まずは掛け算をする・・・ 8×2=16
データは2個なので、2乗根を計算する・・・ √16=4
「8」と「2」の幾何平均は、「4」になります。
例②:「4」と「8」と「2」の幾何平均を求める
まずは掛け算をする・・・ 4×8×2=64
データは3個なので、3乗根を計算する・・・ ∛64=4
「4」と「8」と「2」の幾何平均も、「4」になります。
【補足】
「う~ん… 覚えられない…」という方は、「単位」をイメージしてみてください。
例②の3つのデータの単位が、「m (メートル)」だったとします。3つのデータをすべて掛けると、単位は「㎥」となりますよね。この「㎥」を「m」に戻すために、3乗根を使用するんだ!と考えると、覚えやすいですよ!
幾何平均の応用例
幾何平均の応用例に、「上昇率」があります。
売上の上昇率、給料の上昇率、物価の上昇率などなど。
ここでは、売上の上昇率を例に説明します。
問題:下記の通り、売上の上昇率が提示された。平均何%ずつ上昇したと言えますか?
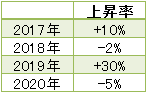
上昇率の平均は「幾何平均」を使う!
よし!習った通り全て掛けて… と、残念ながらそうはいきません。
幾何平均の考え方は、
「X倍!Y倍!Z倍!これをならすと、1回あたりは、∛XYZ倍!」
というものなので、○○倍の形に変換しなければなりません。
(そもそも、幾何平均は「マイナス」が扱えないんですよね…)
というわけで、前年から何倍になっているのかで表示します。
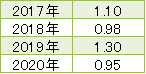
ここから計算スタートです。
まずは掛け算をする・・・ 1.10×0.98×1.30×0.95≒1.33
データは4個なので、4乗根を計算する・・・ ∜1.33≒1.07
幾何平均は「1.07」!
つまり、この4年間は平均「+7%」ずつ上昇したことになります。
幾何平均の発展
問題:下記の通り、売上が提示された。
2016年から2020年にかけて、平均何%ずつ上昇したと言えますか?
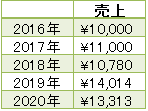
こちらは、前章の上昇率が提示されず、売上データが提示されたパターンになります。こちらの方が、一般的ですね。
先に、算出方法から示します・・・ ∜(13313/10000)≒1.07
2016年から4年かけて、¥10,000→¥13,313と上昇しました。
従って、4年間の上昇は「1.3313倍」、1年平均の上昇は「∜1.3313倍」となります。
上記の式は、前章の手法からも導くことができます。
「まずは掛け算をする」ということで、前年から何倍になっているか をすべて掛けた式を作成します。
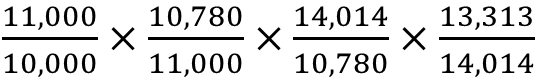
順に、2016年→2017年で何倍になったか、2017年→2018年で何倍になったか、2018年→2019年で何倍になったか、2019年→2020年で何倍になったか、を掛けています。
この式は約分できるので、下記の通り削除します。

最後に、データが4個なので、4乗根を計算すると、∜(13313/10000) の式が導かれます。
おわりに
普段の生活では、めったに使わない幾何平均ですが、投資をしている人、これから投資をしようと考えている人は、覚えてみてください!
企業の売上が、平均どのくらいの上昇率なのか確認するときに使用できますよ!
投資をしない人?
テストかなんかが終わったら忘れましょう!






コメント