相関係数とは
相関係数は、2変数間の線形関係の程度を表す係数です。
相関係数の値の範囲は、-1から+1です。
符号が「+」であれば、正の相関 ( 片方が大きくなれば、他方も大きくなる関係 )、
符号が「-」であれば、負の相関 ( 片方が大きくなれば、他方は小さくなる関係 )を表します。
また、絶対値が「1」に近いほど、より強い線形関係を表しています。
相関係数の求め方
相関係数の計算式
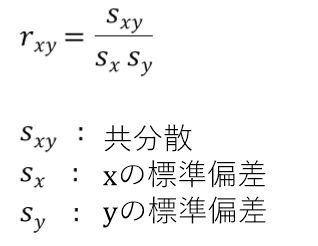
( 同じ記号なのに、分子は分散、分母は標準偏差を表しているので注意です。 )
分母には、2変数それぞれの標準偏差を使用します。
標準偏差について知りたい場合は、是非、参考記事をご確認ください。
相関係数の算出例
次のような、年齢と給料のデータがあります。
相関係数を求めてみましょう。
なお、年齢の平均値は「34歳」、給料の平均値は「30.5万」です。

①共分散を求める
それぞれの偏差 ( 平均値からの差 ) を掛けた値の平均値です。
{(20-34)(20-30.5)+(27-34)(25-30.5)+(39-34)(37-30.5)+(50-34)(40-30.5)} ÷ 4 = 92.5
②各変数の標準偏差を求める
偏差 ( 平均値からの差 ) の2乗の平均値をルートした値です。
年齢:√[{(20-34)^2+(27-34)^2+(39-34)^2+(50-34)^2}÷ 4] ≒ 11.467
給料:√[{(20-30.5)^2+(25-30.5)^2+(37-30.5)^2+(40-30.5)^2}÷ 4] ≒ 8.261
③相関係数の計算式に代入する
92.5 ÷ (11.467 × 8.261) ≒ 0.976
相関係数は「0.976」となりました。
絶対値が「1」に近いため、かなり強い相関があると言えます。
解釈の注意点
相関関係は因果関係とは異なる
相関係数の絶対値が「1」に近いほど、強い相関関係があると言えます。
ここで注意したいのは、「相関関係」は「因果関係」ではないということです。
例えば、あるダイエット水について、
「飲む回数が多い人は、体重が減る」という結果が得られたとします。
ここに相関関係はありますが、因果関係は不明です。
ダイエット水を飲むことで、ダイエット意識が向上し、よく階段を使用するようになっていたのなら、体重の減少と因果関係があるのは、「適度な運動」となります。
このように、相関係数から直接、因果関係を述べることはできないので、2つの変数が持つ背景については、よく考察する必要があります。
曲線の関係については分からない
相関係数は、直線的な関係を表現しています。
従って、曲線的な関係があったとしても、絶対値は「1」に近づきません。
相関係数の絶対値が「1」に近くない場合でも、2変数間に全く関係がないとは言えませんので、可能であれば散布図まで確認するようにしましょう。
おわりに
相関係数は、線形関係の程度を表す便利な指標ですが、考察においては注意が必要です。
2つの変数にどのような背景があるのか、第3の関連因子はないか など注意深く考察するようにしましょう。
きっとデータに強い人になれるはずです!








コメント