中心極限定理とは
この定理は、「母集団の分布の形状によらず、
そこから抽出した標本の平均値は、正規分布に従う」というものです。
平均値算出の際のデータ数(標本サイズ)は、大きいほど正規分布に従います。
母集団が、平均μ、分散σ^2の確率分布に従う場合、
標本平均の分布は、平均μ、分散σ^2/nの正規分布に近づきます。
具体例で解説
( どんな分布でもいいのですが ) 例えば、イカサマ用のコインがあるとします。
表が出る確率が30%、裏が出る確率は70%です。
表が出ることを「1」、裏が出ることを「0」と表すと、以下の確率分布となります。
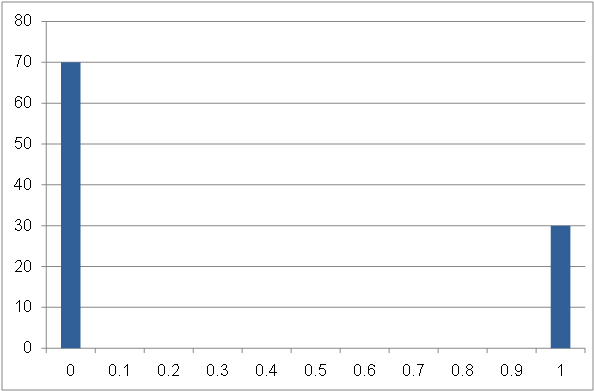
このコインをN回投げた時の平均値について、何度も確認します。
( 10回投げた結果が、0、0、1、0、1、1、0、0、0、0 なら、平均値は0.3ですね )
その時のヒストグラムが、次のようになりました。

1( =表 )が出る確率が30%なので、平均値0.3の回数が多かったようです。
中心極限定理はこのように、平均値の分布が、正規分布になるという定理です。
なお、Nの回数( 標本サイズ )を増やすほど、より正規分布に近づき、
より真の発生割合( 上記の例では「0.3」)に多く分布するようになります。
今回、母集団の分布を、2値の確率分布としましたが、
2値の確率分布でなくても成り立つ法則です。
メリットは何か
何かの優劣を比較するとき、平均値を比較することがあります。
標本平均が正規分布を描くことで、平均値の区間推定ができたり、
母集団が正規分布でなくても t検定が近似的に行えたりと、
中心極限定理の存在のメリットは大きいです。







コメント