ローレンツ曲線とジニ係数とは
偏り(=集中度あるいは格差)を表すためのグラフが「ローレンツ曲線」で、
そのような不平等さを、数値で表したのが「ジニ係数」です。
ローレンツ曲線
ローレンツ曲線は、度数と値の累積相対度数の関係をプロットすることで、
作成することができます。
ここでは例として、架空の500世帯の月収について作成してみます。
作成手順は、以下のとおりです。
①世帯を月収の低い順に並べる
②世帯をいくつかの階級に分ける (ここでは5つ)
③度数と値の累積相対度数を求める
④プロットする (横軸:度数 (世帯数)、縦軸:値 (月収))
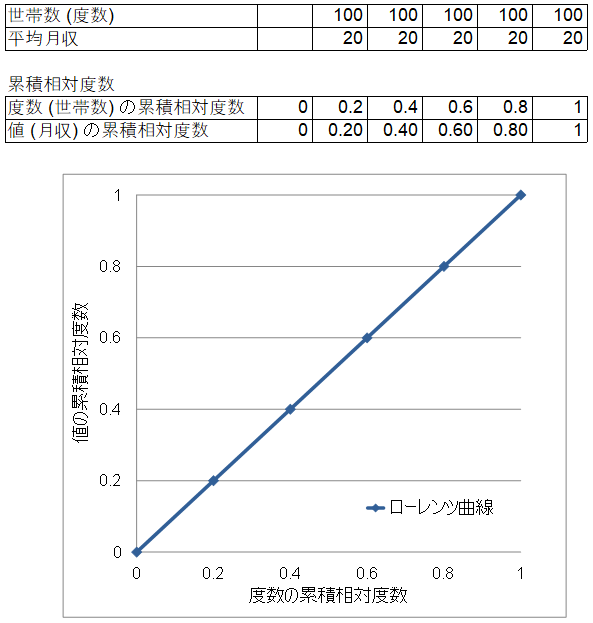
【補足】
値 (月収) の累積相対度数の求め方は、
まず全世帯分 (500世帯) の収入を計算します。
(20×100+20×100+20×100+20×100+20×100=10,000万円)
その中で、各階級が占める収入を考えていきます。
(1つ目の階級なら、20×100=2000万を占めるため、 2000÷10,000=0.2)
後は、通常の累積相対度数の求め方と同じです。
(世帯数が均等だと分かりづらいので、補足しました。)
この例は、全ての世帯の月収を20万円としました。
従って、全階級の平均月収も20万になり、階級が上がるにつれ
均等な上昇を見せています。
このように、均等なデータだと、
ローレンツ曲線は、45°一直線のグラフになります。
次は、偏りのあるデータをグラフ化してみます。

偏りのあるデータをグラフ化すると、
45°の直線 (黒色点線:「完全平等線」という) から歪みました。
この例ですと、収入の低い方から20%の世帯数 (100世帯) を抽出しても、
月収は全体の8%分しか抽出されていないということです。
(偏ってますねぇ)
ローレンツ曲線は、完全平等線から歪めば歪むほど、
値 (月収) に偏りがあると判断できます。
ジニ係数
ジニ係数は、ローレンツ曲線で表される偏りを、数値で表すもので、
以下の式で求まります。
ジニ係数=(完全平等線とローレンツ曲線で囲んだ面積(赤色))×2
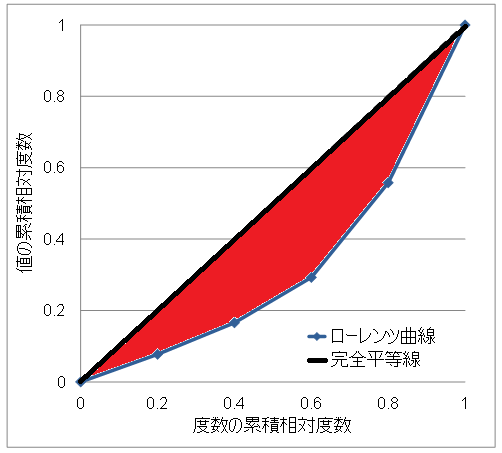
日本統計学会作成の「統計検定2級対応 統計学基礎」によると、
「ジニ係数=(正方形に対する赤色面積の”割合”)×2」となっていますが、
正方形の面積は「1」なので、単純に「赤色面積の2倍」で覚えた方が楽ですね。
ジニ係数は、0~1の値を取り、
0は完全に均等である状態で、1は全くの不均等な状態です。
今回の例だと、以下のような場合です。
0:全世帯の月収が同じ。(最初に説明したローレンツ曲線のグラフ)
1:400世帯超の月収が0円で、一部世帯のみ月収がある。(世紀末)
なお、ジニ係数は、面積 (細かく言うと面積の「割合」) より求まるため、
ジニ係数が同じであっても、ローレンツ曲線の形状まで同じとは限りません。
まとめ
偏り(=集中度あるいは格差)を表すためのグラフが「ローレンツ曲線」で、
そのような不平等さを、数値で表したのが「ジニ係数」でした。
ローレンツ曲線は、度数と値の累積相対度数を求めて、
それをプロットすることで作成できます。
ジニ係数は、「(完全平等線とローレンツ曲線で囲んだ面積(赤色))×2」で
求めることができます。







コメント