分散とは何か
分散とは、値のバラツキ具合を表現する統計量になります。
データが、平均値から遠くまで散らばっていればいるほど大きな値を算出します。
後述の計算式より分かるとおり、分散の単位は、元の単位の2乗になります。
単位が変わると分かりづらいので、データの要約の際は、
分散をルートした「標準偏差」の方がよく使われます。
分散の求め方
分散の式は、2種類あります。( といっても、微調整程度の違いです )
実際にデータを扱う際は、サンプルサイズ( n ) が大きいことが多く、
意識しなくても、結果は大差ありません。
統計検定を受ける場合など、学問として学ぶ場合は意識しましょう。
分散 ( 記述統計 統計検定3級 )

分母がnの分散です。
目の前にあるデータのみに興味があり、
データの要約をしたいときには、こちらの分散式を用います。
例えば、とある学年から人気者の5人の生徒の身長を把握できました。
この5人の身長について、散らばりを把握する場合が該当します。
計算ステップを具体例を使って説明します。
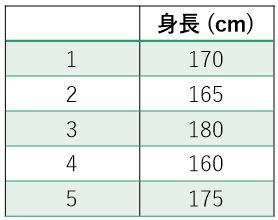
① データの平均値を算出する。
(170+165+180+160+175)/5=170
② 各データの値から、①で求めた平均値を引き、それを2乗する。
(170-170)^2=0、(165-170)^2=25、(180-170)^2=100、
(160-170)^2=100、(175-170)^2=25
③ 全部のデータで②の処理を行ったら、すべて足し合わせる。
0+25+100+100+25=250
④ ③で得た値を、データの数で割る。
250/5=50 (cm^2)
分散は、50 (cm^2)となりました。単位は、元のcmの2乗になります。
不偏分散 ( 推測統計 統計検定2級 )

分母が(n-1)の分散です。
目の前にあるデータ (標本) から、母分散を推測したいときに用います。
例えば、とある学年からランダムに5人の生徒の身長を把握できました。
この5人の身長から、学年全体の身長の分散 (母分散) を推測する場合が該当します。
計算の流れは前項と同じですが、最後に(データの数-1)で割るところのみ異なります。
① データの平均値を算出する。
② 各データの値から、①で求めた平均値を引き、それを2乗する。
③ 全部のデータで②の処理を行ったら、すべて足し合わせる。
④ ③で得た値を、(データの数-1) で割る。
一致性と不偏性
母集団の推定量には、「一致性」と「不偏性」という2つの判断基準が存在ます。
・一致性:サンプルサイズ( n )が大きい時、真の値に近づく性質
・不偏性:推定量の期待値が、真の値である性質
各分散についての判定は、以下のとおりです。
・分散:一致性あり、不偏性なし (母分散の一致推定量)
・不偏分散:一致性あり、不偏性あり (母分散の一致推定量&不偏推定量)
これより、推定量を求める場合は、不偏分散が適しています。
( 不偏性がなければ、推定量として使い物にならないという話ではないです。 )
まとめ
分散とは、値のバラツキ具合を表現する統計量で、
単位は、元データの単位の2乗になります。
計算の際の分母は、算出された値の利用方法により異なります。
分母n :データを要約したい。( 記述統計 )
分母n-1:データから母分散を推測したい。( 推測統計 )
nが大きくなると、値はほとんど変わりませんが、
間違えると細かい人に怒られるので、気にしてみましょう!








コメント