【統計】四分位数と四分位範囲とは？求め方をしっかり解説！

四分位数とは

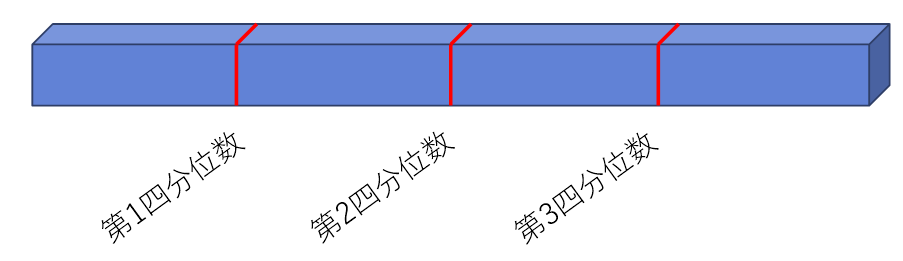
データを小さい方から並べて、データを「個数」で四分割したとき、
境界部分を担当する「値」のことです。

四分位数は、値が小さい方から、
「第1四分位数」「第2四分位数」「第3四分位数」と呼ばれます。

もし、境界部分に値がない場合は、境界前後の値の平均値になります。

いくつか例を挙げます。
　

「1 1 2 2 5 6 6 7 7 8 9」
第1四分位数：2、第2四分位数：6、第3四分位数7

「1 1 2 2 5 6 6 7 7」
第1四分位数：1.5、第2四分位数：5、第3四分位数6.5

「1 1 2 2 5 6 6 7」
第1四分位数：1.5、第2四分位数：3.5、第3四分位数6
　

なお、「第2四分位数」の定義は「中央値」と同じで、同値です。

四分位数を求める場合は、まず「第2四分位数」を求めます。
(データ数を2分割する境目の値。なければ境目前後の平均値。)
「1 1 2 2 5 6 6 7 7」
　

第2四分位数が分かったら、
第2四分位数より前のデータと第2四分位数より後のデータに分けて考えます。
(第2四分位数は、選択肢から除きます。)

前のデータ「1 1 2 2」
後のデータ「6 6 7 7」
　

前のデータ、後のデータそれぞれで中央値を求めます。
(データ数を2分割する境目の値。なければ境目前後の平均値。)

前のデータ「1 1 2 2」→第1四分位数：1.5
後のデータ「6 6 7 7」→第3四分位数：6.5
　

このような順で、求めることができます。

いきなり4等分を目指すのではなく、半分にしてから更に半分にする手順は、
実生活で4等分したい時と同じですね。
(豆腐とかケーキとかのカット手順)

四分位範囲は、第1四分位数から第3四分位数の範囲であり、
値は、第3四分位数から第1四分位数を引いた値になります。

前項の例を使うと、
6.5-1.5=5 より、四分位範囲は「5」になります。
　

四分位数はデータ数を4等分するための値なので、
第1四分位数から第3四分位数の範囲 ( 四分位範囲 )には
全体の半分( 50% )のデータ数が含まれることになりますね。

ちなみに、四分位範囲は、データのバラツキを表現する値です。
通常のデータの「範囲」( 最大値 – 最小値 )でバラツキを確認しようとすると、
「外れ値」の影響をダイレクトに受けます。

四分位範囲は、外れ値の影響を避けるために、
全体の真ん中50%のデータを使って、バラツキを表現しています。

従って、四分位範囲は、
外れ値の影響をほとんど受けないバラツキの指標となっています。

四分位数は、データを小さい方から並べて、
データを「数」で四分割したときに、境界部分を担当する「値」のことです。

四分位数は3つあり、小さい方から、
「第1四分位数」「第2四分位数」「第3四分位数」と呼ばれます。

四分位範囲は、データのバラツキを表現する値で、
第1四分位数から第3四分位数の範囲を指します。
普通の「範囲」より渋い範囲ですね。

　
四分位数、四分位範囲を理解できたら、
あわせて「箱ひげ図」も理解するようにしてください。